Proofs — basic strategies for proving universal statements (CSCI 2824, Spring 2015)
It is often enlightening to learn from mistakes. On this page, we study examples of wrong proofs (and hopefully learn to not repeat them in homework/exams!).
Flawed Mathematical Arguments
We will now see examples of flawed arguments that you need to watch out for when doing mathematics. Examples include
- Proving by example: Just present a few examples and note that an universal statement holds based on these.
- Assuming some fact in the proof that does not follow from the premise.
- Proving by intuition: Appeal to your intuition usually by drawing a diagram.
- Statements that should never be present in a good proof:
- it is clear to me (proof by vision!! )
- it just feels right (the touchy-feely proof!! )
- intuitively,… (proof by intuition!! )
- my professor told us that,… (proof by authority!! )
- it is obvious. (unless it truly truly truly is rather obvious as 1+1 = 2 !!).
- Proving the wrong statement.
- Proof of the converse (instead of proving
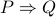 , we prove
, we prove 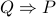 ).
).
- Proof of something unrelated.
- Not proving the statement for all the cases.
- Missing out on some corner cases.
- Proof only applies to
 even but not to
even but not to  odd.
odd.
Example# 1
Claim: For 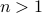 , if
, if  is even, then
is even, then 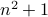 is prime. I.e,
is prime. I.e, 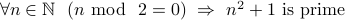 .
.
Proof Attempt # 1
Let us test for 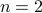 , we have
, we have 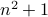 is 5. Works. It also works for
is 5. Works. It also works for 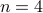 since
since 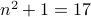 is prime and
is prime and 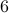 since
since 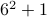 is prime. Therefore,
is prime. Therefore, 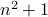 is prime if
is prime if  is even.
is even.
Let us attempt one more proof of this:
Proof Attempt # 2
Assume 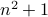 is prime. We will prove that
is prime. We will prove that  must be even.
must be even.
- Since
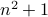 is prime, and
is prime, and 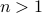 ,
, 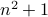 must necessarily be odd.
must necessarily be odd.
- Since
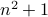 is odd, it must be the case that
is odd, it must be the case that 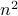 is even.
is even.
- If
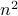 is even, we have proved previously that
is even, we have proved previously that  is also even.
is also even.
- Therefore,
 is even. QED??
is even. QED??
Are there any flaws in either of these proofs? Do they convince you of the truth of our “claim”?
Answer
The claim is false in the first place because it fails for 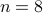 , wherein
, wherein 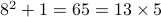 .
.
The first proof attempt is a proof by example which is generally invalid for universally quantified statements.
The second proof attempt actually sets out to prove the converse. Instead of proving 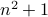 is prime, it assumes this and tries to prove, instead, that
is prime, it assumes this and tries to prove, instead, that  is even.
is even.
Example #2
Claim If two numbers  and
and 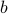 are odd, then
are odd, then 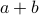 is even.
is even.
Exercise: Write this down in logical notation.
Let us look at a proof:
Attempted Proof
Proof Here are our reasoning steps:
- Since
 is odd, it can be written as
is odd, it can be written as 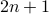 for some
for some  .
.
- Since
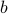 is odd, it can be written as
is odd, it can be written as 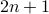 too for some
too for some  .
.
- Therefore
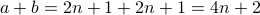 .
.
- But
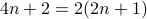 is an even number.
is an even number.
- Therefore,
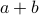 is even. QED.
is even. QED.
Is there anything wrong with the proof above?
Now let us look at a related claim:
Claim-2 If two numbers  and
and 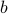 are odd, then
are odd, then 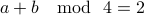 .
.
Is this a true statement?
Here are our reasoning steps:
- Since
 is odd, it can be written as
is odd, it can be written as 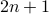 for some
for some  .
.
- Since
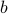 is odd, it can be written as
is odd, it can be written as 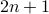 too.
too.
- Therefore
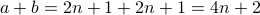 .
.
 .
.- Therefore,
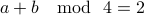 . QED.
. QED.
Can you correct the demonstrations above? What went wrong.
Answer
The problem was in assuming that 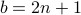 for some
for some  . By saying that
. By saying that 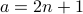 , for some
, for some  and
and 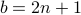 for some
for some  , there is a flawed assumption that
, there is a flawed assumption that 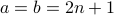 , which was never warranted.
, which was never warranted.
Therefore, we are able to “prove” Claim-2, which is clearly false. For example,  and
and  yields us
yields us  and
and 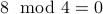 .
.
Claim-1 is correct and the corrected proof is as follows:
Claim-1 If two numbers  and
and 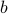 are odd, then
are odd, then 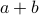 is even.
is even.
Corect Proof
Proof Here are our reasoning steps:
- Since
 is odd, it can be written as
is odd, it can be written as 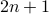 for some
for some  .
.
- Since
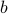 is odd, it can be written as
is odd, it can be written as 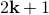 too for some
too for some 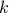 .
.
- Therefore
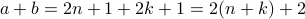 .
.
- But
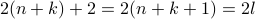 is an even number.
is an even number.
- Therefore,
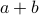 is even. QED.
is even. QED.
Example #3
Claim If  is natural number then
is natural number then 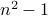 is a composite number.
is a composite number.

Proof: Let be a natural number.
- We can write
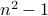 as a product of
as a product of  .
.
- Therefore
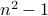 is a composite number. QED??
is a composite number. QED??
Answer
The claim is actually false. Take 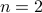 , we have
, we have 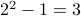 , a prime number.
, a prime number.
What went wrong in the proof? Well, we are correct in writing as  but this does not immediately show that
but this does not immediately show that 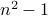 is composite. We have to convince ourselves that
is composite. We have to convince ourselves that 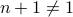 and
and 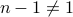 . Recall:
. Recall:
Definition: Prime and Composite Numbers
A natural number  n geq 2" />is composite if it can be written as
n geq 2" />is composite if it can be written as 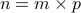 for natural numbers
for natural numbers 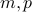 where
where 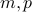 cannot be
cannot be  or
or  itself. In logic, we define a predicate
itself. In logic, we define a predicate 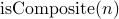 as follows:
as follows:
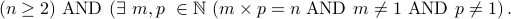 n geq 2) mbox
n geq 2) mbox
(exists m,p in mathbb ( m times p = n mbox m not= 1 mbox p not= 1),." />.
Likewise, natural number  n geq 2" />is prime if
n geq 2" />is prime if 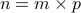 for some natural numbers
for some natural numbers 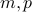 , then
, then  or
or 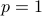 . In logic, we define a predicate
. In logic, we define a predicate 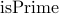 for natural numbers, as follows:
for natural numbers, as follows:
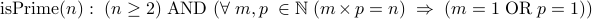 n geq 2) mbox (forall m,p inmathbb ( m times p = n) Rightarrow ( m = 1 mbox p = 1) )" />
n geq 2) mbox (forall m,p inmathbb ( m times p = n) Rightarrow ( m = 1 mbox p = 1) )" />
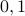
An important exception involves the numbers . These are taken to be neither prime nor composite.
The proof above can only be correct when 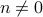 and
and 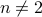 .
.

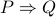 , we prove
, we prove 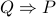 ).
). even but not to
even but not to  odd.
odd.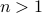 , if
, if 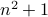 is prime. I.e,
is prime. I.e, 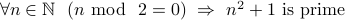 .
.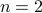 , we have
, we have 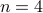 since
since 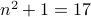 is prime and
is prime and 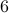 since
since 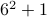 is prime. Therefore,
is prime. Therefore, 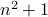 is prime if
is prime if 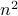 is even.
is even.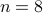 , wherein
, wherein 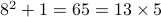 .
. and
and  are odd, then
are odd, then  is even.
is even.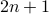 for some
for some 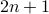 too for some
too for some 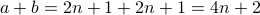 .
.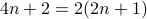 is an even number.
is an even number.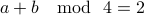 .
. .
.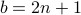 for some
for some 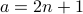 , for some
, for some 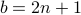 for some
for some 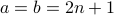 , which was never warranted.
, which was never warranted. and
and  yields us
yields us  and
and 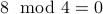 .
.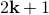 too for some
too for some 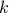 .
.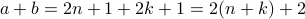 .
.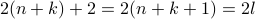 is an even number.
is an even number.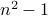 is a composite number.
is a composite number.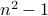 as a product of
as a product of  .
.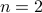 , we have
, we have 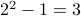 , a prime number.
, a prime number. but this does not immediately show that
but this does not immediately show that 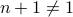 and
and 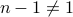 . Recall:
. Recall: n geq 2" />is composite if it can be written as
n geq 2" />is composite if it can be written as 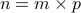 for natural numbers
for natural numbers 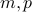 where
where  or
or 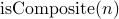 as follows:
as follows: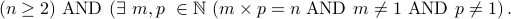 n geq 2) mbox
n geq 2) mbox or
or 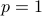 . In logic, we define a predicate
. In logic, we define a predicate 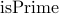 for natural numbers, as follows:
for natural numbers, as follows: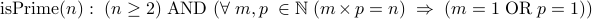 n geq 2) mbox (forall m,p inmathbb ( m times p = n) Rightarrow ( m = 1 mbox p = 1) )" />
n geq 2) mbox (forall m,p inmathbb ( m times p = n) Rightarrow ( m = 1 mbox p = 1) )" />
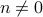 and
and 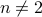 .
.